Question: Following data correspond to an orthogonal turning of a 100mm diameter rod on a lathe. The orthogonal rake angle is +15°; the uncut chip thickness is 0.5mm, the nominal chip thickness after the cut 1.25mm. What is the shear angle for this? [GATE 2018]
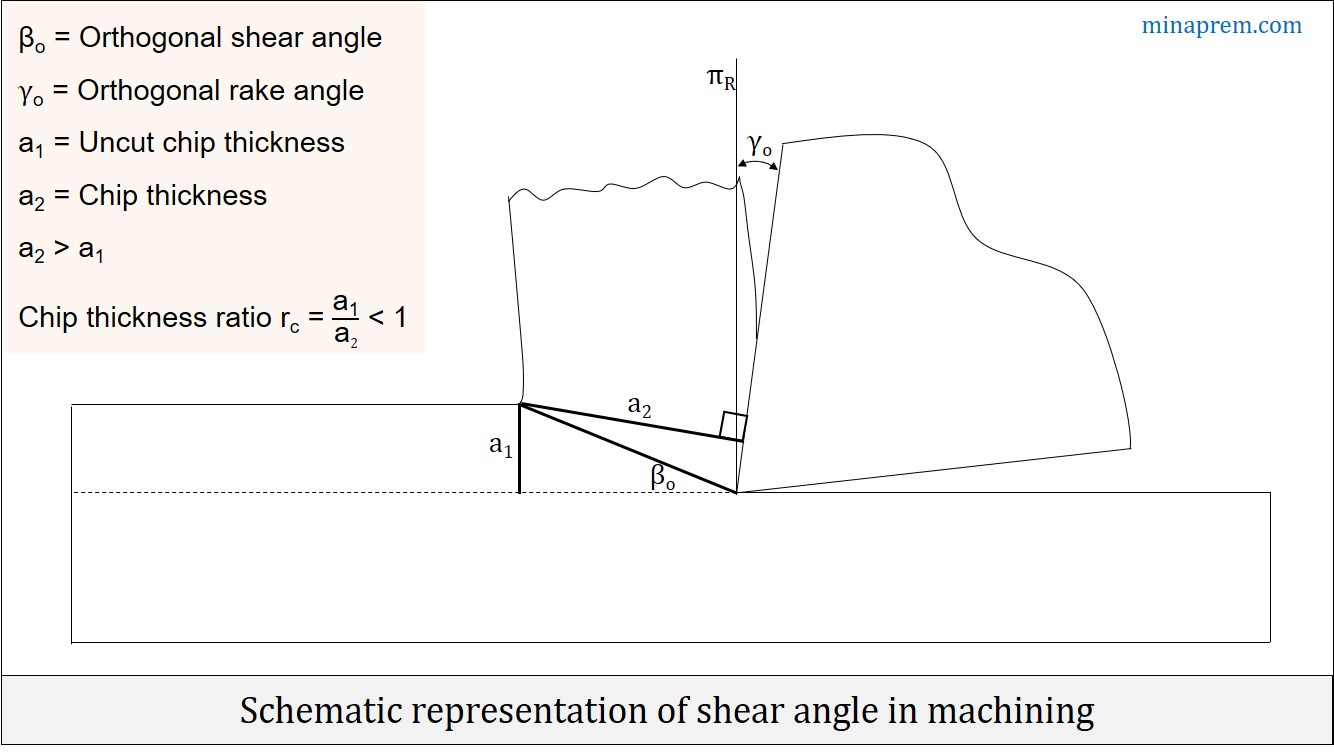
Solution: Shear angle (βo) indicates the direction of shear plane with respect to cutting velocity (Vc) vector. During any conventional machining process, the cutting tool compresses a thin layer of workpiece material and gradually removes it in the form of chip. Material removal takes place by shearing as a layer of workpiece material ahead of the tool slides over another layer and subsequently gets converted into chip. Actually this shearing occurs over a broader region; however, it can be assumed as a 2-D plane for the sake of simplicity. Inclination of this shear plane from velocity vector, when viewed in orthogonal plane (πO), is termed as orthogonal shear angle (βo) as shown below.
\[\tan {\beta _O} = \frac{{\cos {\gamma _O}}}{{\zeta – \sin {\gamma _O}}}\]
This orthogonal shear angle (βo) can be expressed in terms of orthogonal rake angle (γo) and chip reduction coefficient (ζ), as given above. The orthogonal rake angle indicates orientation of tool’s rake face from reference plane and measured on orthogonal plane. Since rake angle can be positive, zero or negative, so algebraic sum should be considered. The chip reduction coefficient (ζ) is the ratio between chip thickness (a2) to the uncut chip thickness (a1). Since a2 > a1, so ζ = (a2/a1) > 1. Chip reduction coefficient is inverse to the chip thickness ration (rc).
Given values in the question are
γo = +15°
a1 = 0.5mm
a2 = 1.25mm
∴ ζ = (a2/a1) = (1.25/0.5) = 2.5
\[\tan {\beta _O} = \frac{{\cos 15}}{{2.5 – \sin 15}} = 0.431\]
\[{\beta _O} = 23.32\]
Therefore, shear angle in the given case is 23.32°.