Question: In an orthogonal cutting operation shear angle = 11.31°, cutting force = 900 N and thrust force = 810 N. What will be the shear force? [ESE 2014]

Solution: With the help of Merchant Circle Diagram (MCD), this problem can be solved easily. A typical MCD for positive rake angle is shown below. Here in the question, the main cutting force (P_Z) and thrust force (P_XY) for an orthogonal cutting operation are provided. Using these two values, the angle between P_Z and R can be calculated and also the value of R can be calculated. Value of shear angle is also given. Thus the shear force can be calculated from the value of R. Step by step solution of this problem is discussed below.

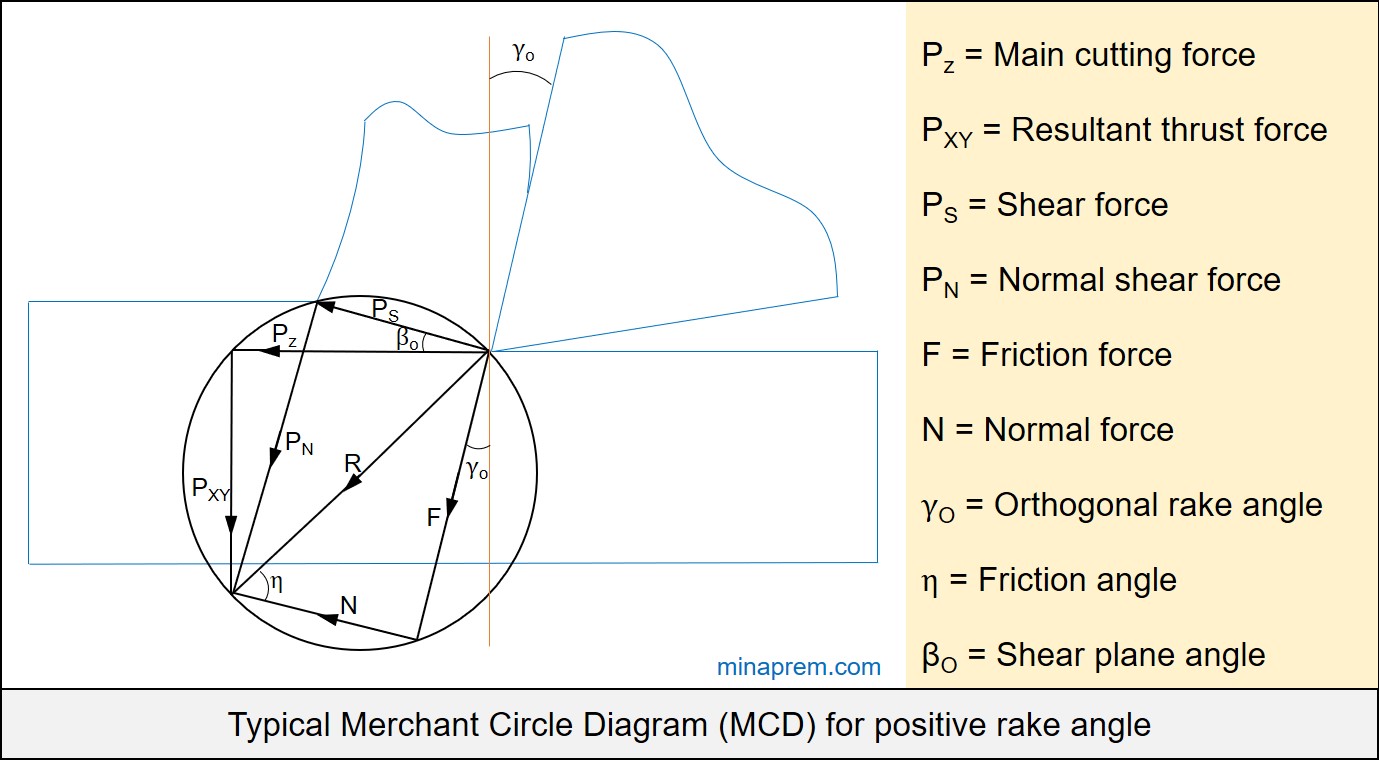
Step-1: Find out the angle between P_Z and R

As shown in above diagram, say the angle between P_Z and R is θ. The triangle constituted by P_XY P_Z and R is one right angle triangle as R is the diameter of the Merchant’s Circle. Thus the value of θ can be easily calculated from the known values of P_XY and P_Z as given below.

\[\tan \theta  = \frac{{{P_{XY}}}}{{{P_Z}}}\]

\[\tan \theta  = \frac{{810}}{{900}} = \frac{9}{10}\]

\[\theta  = {\tan ^{ – 1}}\left( {\frac{9}{10}} \right) = 42^\circ \]

Step-2: Calculate value of resultant force (R)

Once again consider the right angle triangle made by P_XY P_Z and R. Since R is the hypotenuse, so it can be calculated easily as given below.

\[R = \sqrt {{{\left( {{P_Z}} \right)}^2} + {{\left( {{P_{XY}}} \right)}^2}} \]

\[R = \sqrt {{{900}^2} + {{810}^2}}  = 1210.8N\]

Step-3: Calculate value of shear force (P_S)

Here in the question, shear angle (β_O) is given as 11.31°. The angle between P_Z and R is calculated in step-1 as θ = 42°. A close look to the MCD reveals that the angle between P_S and R is (θ + β_O) = (42° + 11.31°) = 53.31°.

Angle between P_S and P_Z = β_O = 11.31°

Angle between P_Z and R = θ = 42°

∴ Angle between P_S and R = (θ + β_O) = (42° + 11.31°) = 53.31°

Now let us consider the triangle made by P_N P_S and R. It is also one right angle triangle with R as hypotenuse. The value of R is calculated earlier. Angle between P_S and R is also known. So the right angle triangle made by P_N P_S and R gives the value of shear force as illustrated below.

\[\cos \left( {\theta  + {\beta _O}} \right) = \frac{{{P_S}}}{R}\]

\[{P_S} = R\cos \left( {\theta  + {\beta _O}} \right)\]

\[{P_S} = 1210.8 \times \cos 53.31 = 723.6N\]

Therefore, the shear force (P_S) for the given orthogonal cutting operation is 723.6 N (Answer).