Question: An orthogonal turning operation is carried out at 20m/min cutting speed, using a cutting tool of rake angle 15°. The chip thickness is 0.4mm and the uncut chip thickness is 0.2mm. Determine (i) the shear plane angle in degrees, and (ii) the chip velocity in m/min. [GATE 2009]

Answer: In conventional machining the workpiece material is removed by shearing as and when the cutting tool compresses it. For simplicity in analysis, it is assumed that sharing takes place in a concentrated 2-D plane. This plane is termed as shear plane. Angle of inclination of this shear plane from the cutting velocity vector is called shear plane angle (β_O). This shear plane angle can be expressed in terms of chip reduction coefficient (ζ) and orthogonal rake angle (γ_O) of the cutting tool, as given below.

\[\tan {\beta _O} = \frac{{\cos {\gamma _O}}}{{\zeta  – \sin {\gamma _O}}}\]

The Chip Reduction Coefficient (ζ) is the ratio between the chip thickness (a₂) to the uncut chip thickness (a₁). So it is one unitless quantity. The chip thickness is usually larger than the corresponding uncut chip thickness (i.e. a₂ > a₁) because of the positive shear strain that exists in machining. Thus Chip Reduction Coefficient is always greater than one, particularly in macro-scale machining. Mathematically,

\[\zeta  = \frac{{{a_2}}}{{{a_1}}} > 1\]

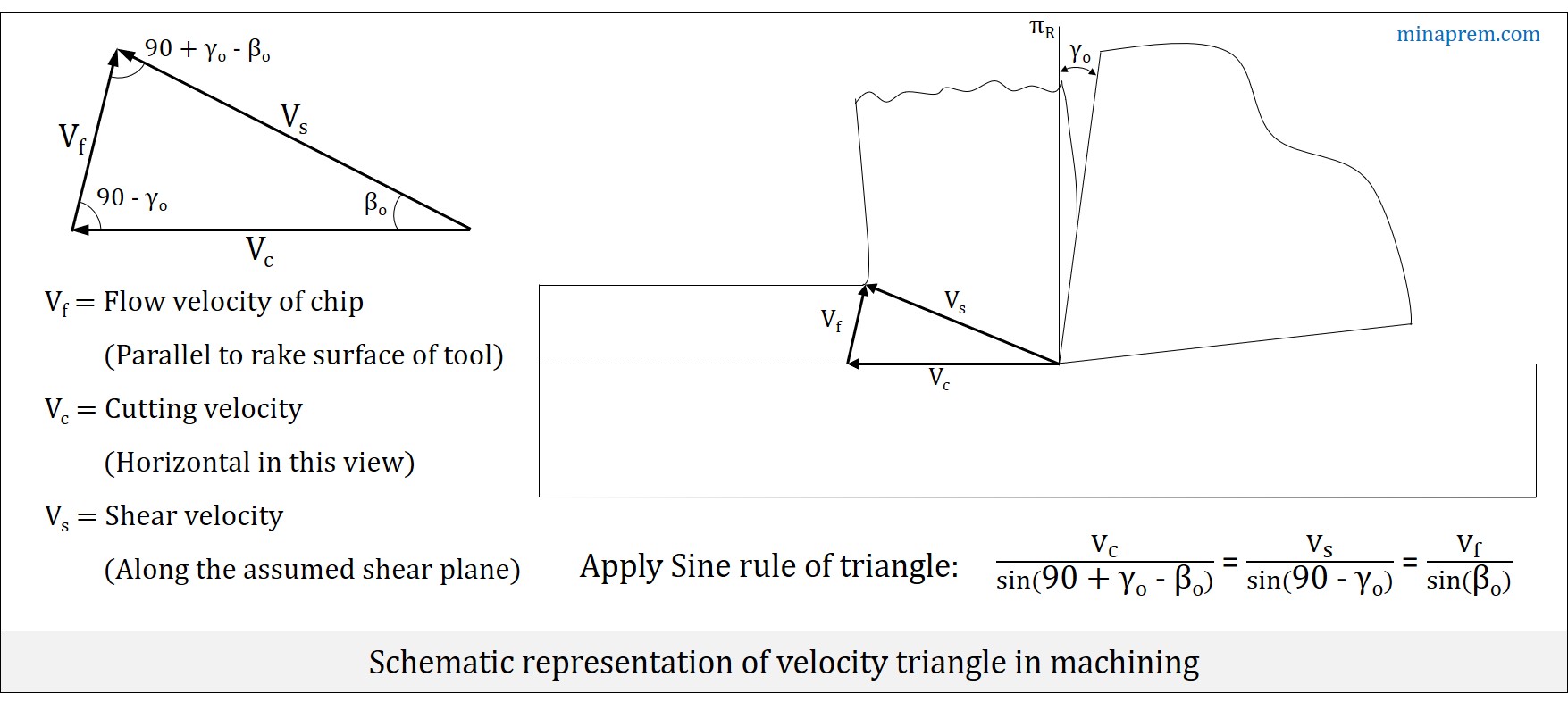
In an orthogonal machining of ductile material with a sharp cutting tool, three velocity parameters namely cutting velocity (V_C), chip flow velocity (V_f) and shear velocity (V_S) together constitute a triangle, as shown below. Since the shear velocity is oriented along the assumed shear plane, the angle between cutting velocity (V_C) and shear velocity (V_S) is nothing but the shear angle (β_O). The chip flow velocity (V_f) is considered along the rake surface and thus its angle with the reference plane is equal to the orthogonal rake angle (γ_O). Thus, angle between cutting velocity (V_C) and chip flow velocity (V_f) is (90° – γ_O). Once two angles of a triangle is known, the third angle can be obtained easily as the sum of all three internal angles of any triangle is 180°. Therefore, application of Sine Rule on the velocity triangle gives the following expression.

\[\frac{{{V_c}}}{{\sin \left( {90 + {\gamma _o} – {\beta _o}} \right)}} = \frac{{{V_s}}}{{\sin \left( {90 – {\gamma _o}} \right)}} = \frac{{{V_f}}}{{\sin {\beta _o}}}\]

Part-1: Calculate shear plane angle

Given, orthogonal rake angle (γ_O) = +15°

Chip thickness (a₂) = 0.4mm

Uncut chip thickness (a₁) = 0.2mm

∴ Chip Reduction Coefficient (ζ) = (a₂ / a₁) = (0.4 / 0.2) = 2.0

Substituting these values, the shear plane angle can be calculated as follows.

\[\tan {\beta _O} = \frac{{\cos 15}}{{2 – \sin 15}} = 0.554\]

\[{\beta _O} = {\tan ^{ – 1}}\left( {0.554} \right) = 29\]

Therefore, shear plane angle for the given case is 29°.

Part-2: Calculate chip velocity

Here, the cutting velocity (V_C) is given as 20m/min and the requirement is chip flow velocity (V_f). Both the orthogonal rake angle (γ_O) and the shear plane angle (β_O) are known. Thus, extracting the V_C and V_f terms from the generalised expression obtained from velocity triangle, the following can be written. Further substituting the values of corresponding parameters, the chip velocity can be obtained.

\[\frac{{{V_c}}}{{\sin \left( {90 + {\gamma _o} – {\beta _o}} \right)}} = \frac{{{V_f}}}{{\sin {\beta _o}}}\]

\[\frac{{20}}{{\sin \left( {90 + 15 – 29} \right)}} = \frac{{{V_f}}}{{\sin 29}}\]

\[{V_f} = \frac{{20\sin 29}}{{\sin 76}}\]

\[{V_f} = 10\]

Therefore, chip velocity for the given case is 10 m/min.