Question: If α is the rake angle of the cutting tool, φ is the shear angle and V is the cutting velocity, then express the velocity of chip sliding along the shear plane in terms of above three parameters. [ESE 2001]

Answer: To solve this question, one need the knowledge of velocity triangle in machining. In an orthogonal machining of ductile material with a sharp cutting tool, three velocity parameters namely cutting velocity (V_C), chip flow velocity (V_f) and shear velocity (V_S) together constitute a triangle, as shown below. If the corresponding angles are known then application of sine rule can provide one or two velocity terms from at least one known velocity.

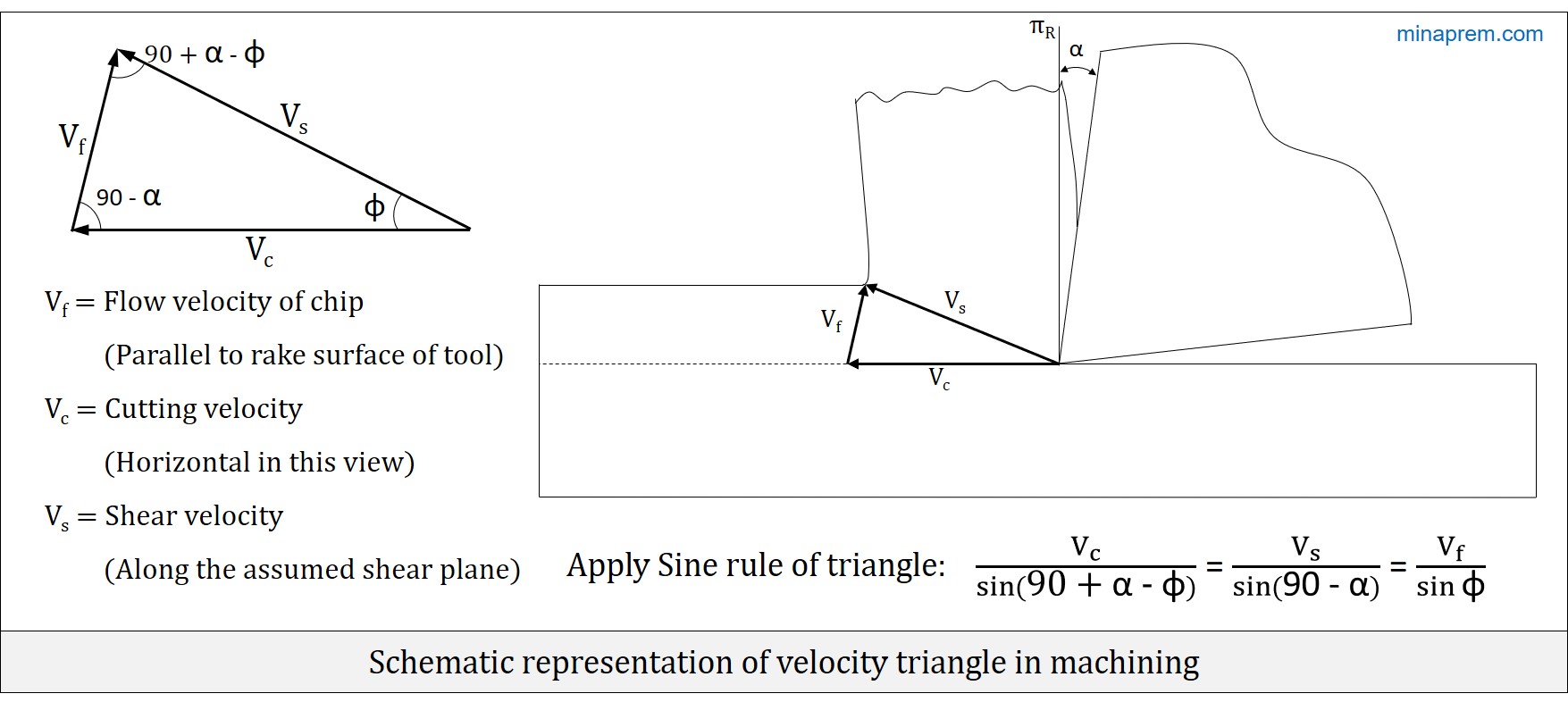
Since the shear velocity is oriented along the assumed shear plane, the angle between cutting velocity (V_C) and shear velocity (V_S) is nothing but the shear angle (φ). The chip flow velocity (V_f) is considered along the rake surface and thus its angle with the reference plane is equal to the orthogonal rake angle (α). Thus, angle between cutting velocity (V_C) and chip flow velocity (V_f) is (90° – α). Once two angles of a triangle is known, the third angle can be obtained easily as the sum of all three internal angles of any triangle is 180°. Therefore, application of Sine Rule on the velocity triangle gives the following expression.

\[\frac{{{V_c}}}{{\sin \left( {90 + \alpha  – \phi } \right)}} = \frac{{{V_s}}}{{\sin \left( {90 – \alpha } \right)}} = \frac{{{V_f}}}{{\sin \phi }}\]

Expressing shear velocity in terms of cutting velocity, orthogonal rake angle and shear angle

The velocity of chip sliding along the shear plane as required in question indicates the shear velocity (V_S). Thus, the objective here is to express the shear velocity in terms of known cutting velocity (V), orthogonal rake angle (α) and shear angle (φ). Eliminating the unnecessary part, the following can be re-written from the generalized formula for velocity triangle.

\[\frac{V}{{\sin \left( {90 + \alpha  – \phi } \right)}} = \frac{{{V_s}}}{{\sin \left( {90 – \alpha } \right)}}\]

\[\frac{V}{{\cos \left( {\phi  – \alpha } \right)}} = \frac{{{V_s}}}{{\cos \left( \alpha  \right)}}\]

\[{V_s} = \frac{{V\cos \alpha }}{{\cos \left( {\phi  – \alpha } \right)}}\]

The above equation expresses velocity of chip sliding along the shear plane as a function of cutting velocity (V), orthogonal rake angle (α) and shear angle (φ).