Calculate shear strain from chip thickness ratio and rake angle

Machining, Numerical

Question: In a machining operation, the chip thickness ratio is 0.3 and the rake angle of the tool is 10°. What is the value of the shear strain? [ESE 2004]

Solution: In any conventional machining process when sample material is ductile, material removal takes place due to shearing under the action of compressive force exerted by the cutting tool. The assumed 2-D plane along which shearing takes place is termed as shear plane; and the inclination of this plane with respect to cutting velocity vector is called shear angle. Moreover, chip thickness after shearing increases as compared to the same for uncut chip before shearing. Accordingly, a positive shear strain exists along the shear plane. This strain is also termed as cutting strain (ε). The average cutting strain as measured in orthogonal plane can be expressed in terms of shear angle (βO) and orthogonal rake angle (γO) of the cutting tool, as displayed below.

\[\varepsilon  = \cot {\beta _o} + \tan ({\beta _o} – {\gamma _o})\]

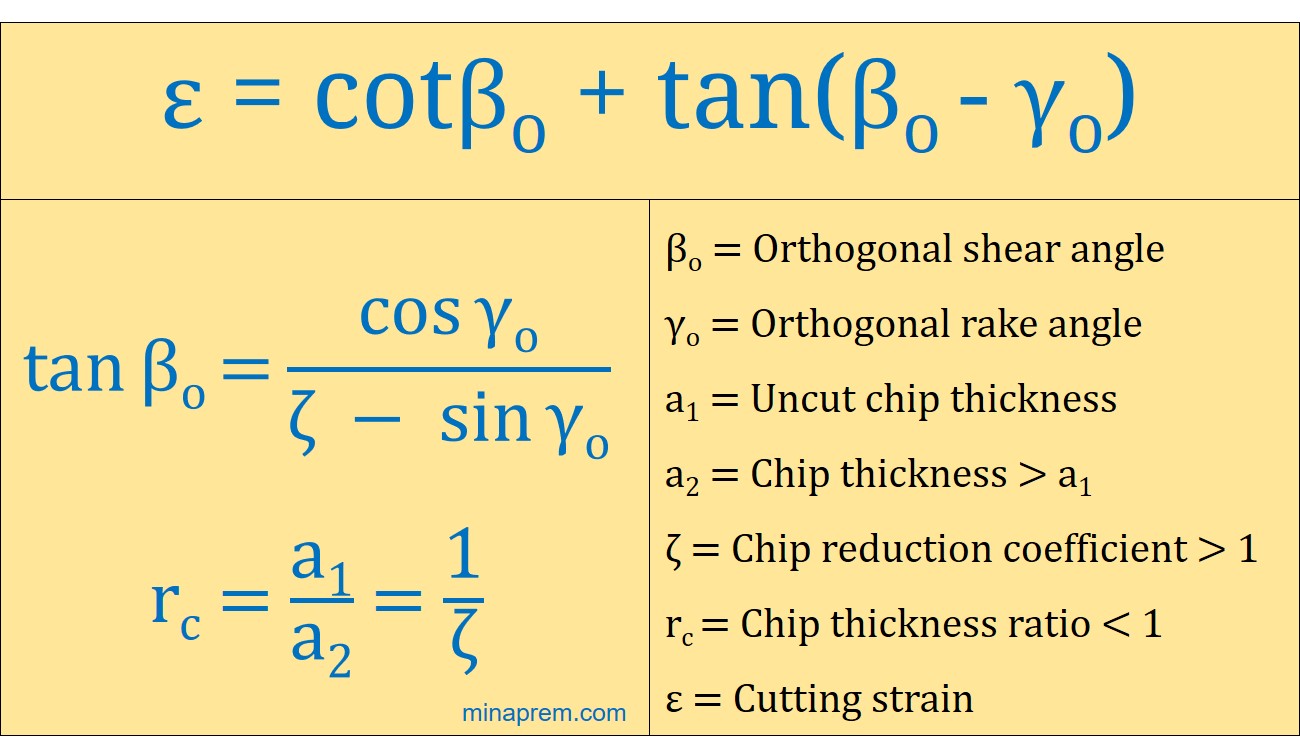
Shear strain formula from chip thickness ratio and rake angle

However, in the question shear angle (βO) is not given; rather the chip thickness ratio (rc) is given. The chip thickness ratio is defined by the ratio between uncut chip thickness (a1) to the chip thickness (a2). Inverse of this is called chip reduction coefficient (ζ). The shear angle (βO) can be expressed in terms of chip reduction coefficient (ζ) and orthogonal rake angle (γO), as displayed below.

\[\tan {\beta _O} = \frac{{\cos {\gamma _O}}}{{\zeta  – \sin {\gamma _O}}}\]

Step-1: Calculate shear angle (βO)

Given, chip thickness ratio (rc) = 0.3

So, chip reduction coefficient (ζ) = (1/rc) = (1/0.3) = 3.33

Orthogonal rake angle (γO) = +10°

Therefore, orthogonal shear angle can be calculated as follows:

\[\tan {\beta _O} = \frac{{\cos 10}}{{3.33 – \sin 10}} = 3.12\]

\[{\beta _O} = {\tan ^{ – 1}}\left( {3.12} \right) = 17.31\]

Step-2: Calculate shear strain (ε)

\[\varepsilon  = \cot 17.31 + \tan (17.31 – 10)\]

\[\varepsilon  = 3.34\]

Therefore, cutting strain for the given conditions is 3.34. Since strain is one unitless quantity (because division of two lengths), so cutting strain is also unitless.

Related posts:

  1. Determine shear strain rate from primary shear zone thickness
  2. Determine ratio between maximum shear angle to minimum shear angle
  3. Determine shear plane angle and chip velocity in orthogonal turning
  4. Calculate shear strain from feed, chip thickness and rake angle
  5. Determine shear angle from orthogonal rake angle and chip thickness ratio
  6. Calculate shear angle using orthogonal rake angle, uncut and cut chip thickness
  7. Shear angle using rake angle, uncut chip thickness and nominal chip thickness
  8. Calculate shear angle for minimum shear strain with positive rake angle
  9. Calculate cutting ratio from chip thickness and feed in turning
  10. Change in chip thickness for doubled feed but constant chip thickness ratio