Question: A single point cutting tool with 12° orthogonal rake angle is used to machine a steel workpiece. The uncut chip thickness is 0.81mm. The chip thickness under orthogonal machining condition is 1.8mm. What is the shear angle? [GATE 2011]

Solution: Machining is one subtractive manufacturing process where layers of material is gradually removed from workpiece by shearing in the form of chips. Shearing actually occurs throughout a 3-D region; however, for the simplicity of analysis, it is assumed that shearing is occurring in a 2-D plane. Inclination of this shear plane from cutting velocity vector is termed as shear angle (β_O). For orthogonal machining, this shear angle can be expressed in terms of Chip Reduction Coefficient (ζ) and orthogonal rake angle (γ_O), as given below.

\[\tan {\beta _O} = \frac{{\cos {\gamma _O}}}{{\zeta  – \sin {\gamma _O}}}\]

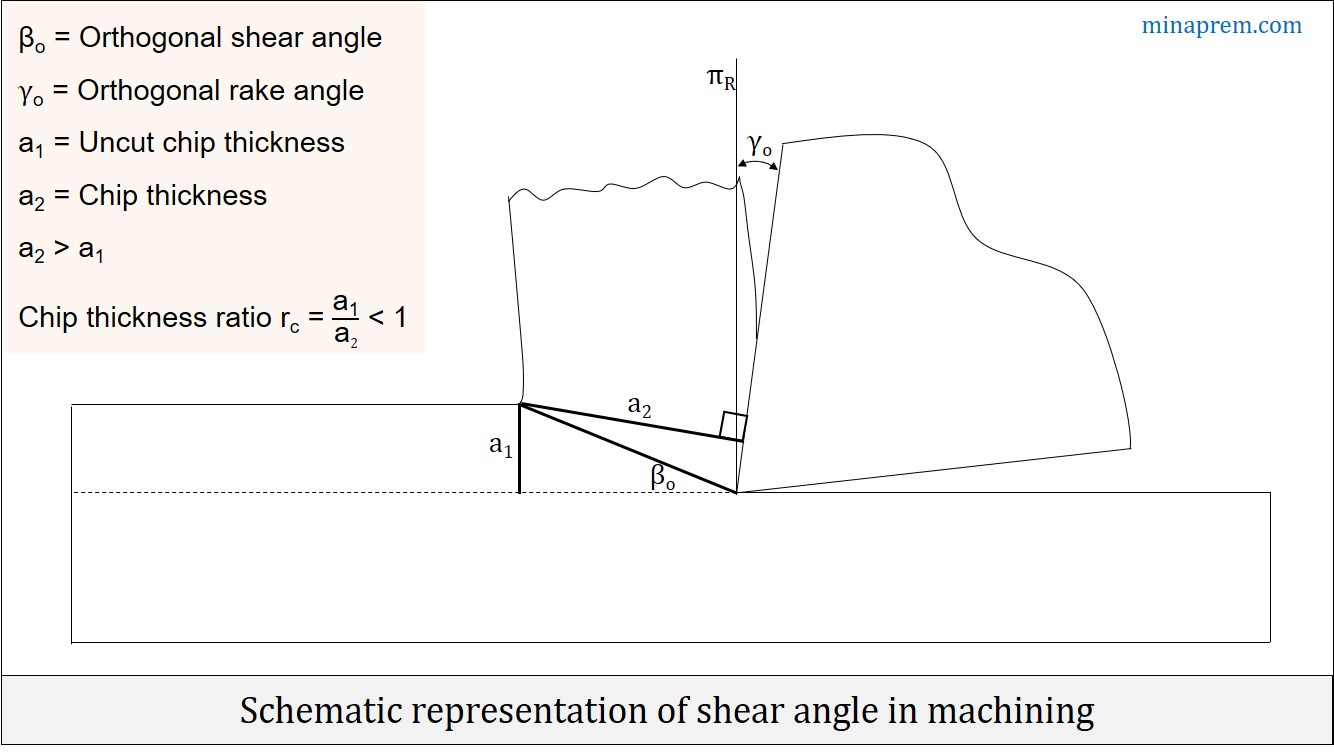
Chip Reduction Coefficient (ζ) is defined as the ratio between the chip thickness (a₂) to the uncut chip thickness (a₁). Due to lamellar flow of the chip under cutting strain, chip gets thickened after shearing; and hence, a₂ becomes larger than a₁. Therefore, ζ > 1. Inverse of the ζ is called chip thickness ratio (r_c). From the given values of a₁ = 0.81mm and a₂ = 1.8mm; let us first calculate Chip Reduction Coefficient. So, ζ = (a₂/a₁) = (1.8/0.81) = 2.22. Now let us apply the above formula of shear angle using the given value of orthogonal rake angle γ_O = 12°.

\[\tan {\beta _O} = \frac{{\cos 12}}{{2.22 – \sin 12}} = 0.486\]

\[{\beta _O} = 25.92\]

Therefore, shear angle in the given case is 25.92°.