Question: A single point cutting tool with 0° rake angle is used in an orthogonal machining process. At a cutting speed of 180 m/min, the resultant thrust force is 490 N. If the coefficient of friction between the tool and the chip is 0.7, then calculate the power consumption for the machining operation. [GATE 2015]

Solution: Cutting power consumption in orthogonal machining can be estimated from main cutting force (P_Z), cutting velocity (V_C), axial feed force (P_X) and chip flow velocity (V_f). The generalized expression for cutting power is given below.

Power = (P_Z V_C) + (P_X V_f)

Usually P_X < P_Z and V_f << V_C, so the effect of axial feed force on cutting power can be neglected. Thus, power can be simply expressed as follows:

Power = P_Z V_C

Here the main cutting force (P_Z) is not directly given, instead the resultant thrust force (P_XY) is given as 490N. So we need to take help of Merchant Circle Diagram (MCD) to determine unknown forces using relevant angles. Here the orthogonal rake angle (γ_O) of the cutting tool is given as 0°. In such scenario, main cutting force (P_Z), resultant thrust force (P_XY), normal force (N) and friction force (F) together form a rectangle, as shown below.

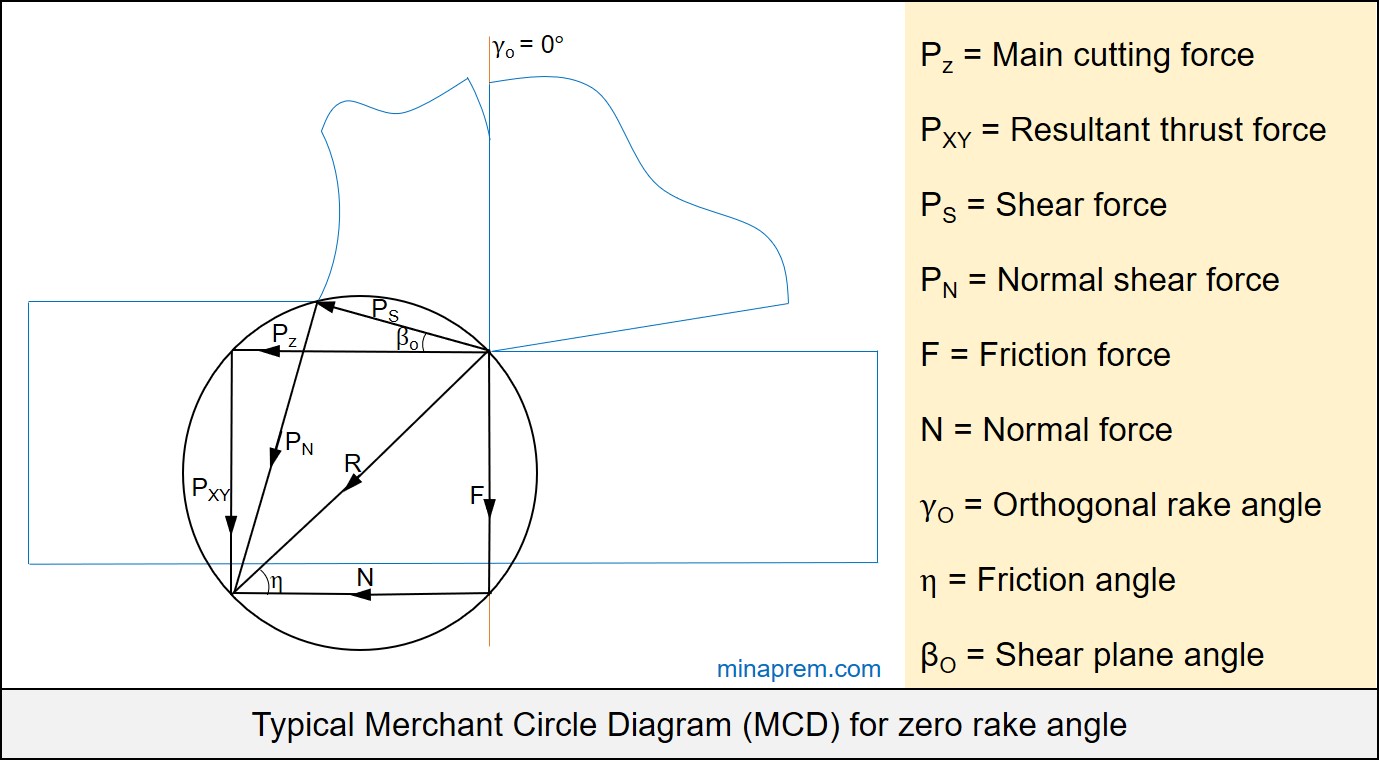
Step-1: Calculate friction angle

The coefficient of friction between the tool and the chip is given as 0.7 (i.e. μ = 0.7). On the other hand, the small angle between the normal force (N) and resultant force (R) in any Merchant Circle Diagram is nothing but the friction angle (η). Moreover, tangent of the friction angle gives the coefficient of friction (μ). So the friction angle can be calculated as follows.

\[\mu  = \tan \eta \]

\[\eta  = {\tan ^{ – 1}}\mu  = {\tan ^{ – 1}}0.7 = 35^\circ \]

Step-2: Calculate main cutting force

In the Merchant Circle Diagram (MCD) for zero rake angle, since P_Z and N are parallel, so the angle between P_Z and R is also equal to friction angle (η). Now let us consider the right angle triangle constituted by P_Z, P_XY and R. Here P_xy is known. So P_Z can be calculated as follows.

\[\tan \eta  = \frac{{{P_{XY}}}}{{{P_Z}}}\]

\[{P_Z} = \frac{{{P_{XY}}}}{{\tan \eta }} = \frac{{490}}{{\tan 35}} = 700N\]

Step-3: Calculate the power consumption

The cutting velocity (V_C) is already given in the question as 180m/min. So V_C = 180m/min = 3m/s. The value of P_Z is also calculated earlier. Therefore, the cutting power consumption for the given case can be calculated as follows.

\[Power = {P_Z} \times {V_C}\]

\[Power = 700 \times 3 = 2100J\]

\[Power = 2.1kJ\]

Therefore, the power consumption for the machining operation is 2.1 kJ.