Question: In an orthogonal cutting process the tool used has rake angle of zero degree. The measured cutting force and thrust force are 500 N and 250 N, respectively. What is the coefficient of friction between the tool and the chip? [GATE 2016]

Solution: This problem can be solved with the help of Merchant Circle Diagram (MCD). MCD is the graphical representation of various forces associated with an orthogonal machining of ductile material under continuous chip formation. It displays shear force (P_S), normal shear force (P_N), main cutting force (P_Z), resultant thrust force (P_XY), friction force (F), normal force (N) and a resultant force (R). It also displays three relevant angles – orthogonal rake angle (γ_O), friction angle (η) and shear angle (β_O). A typical MCD for zero rake angle is given below.

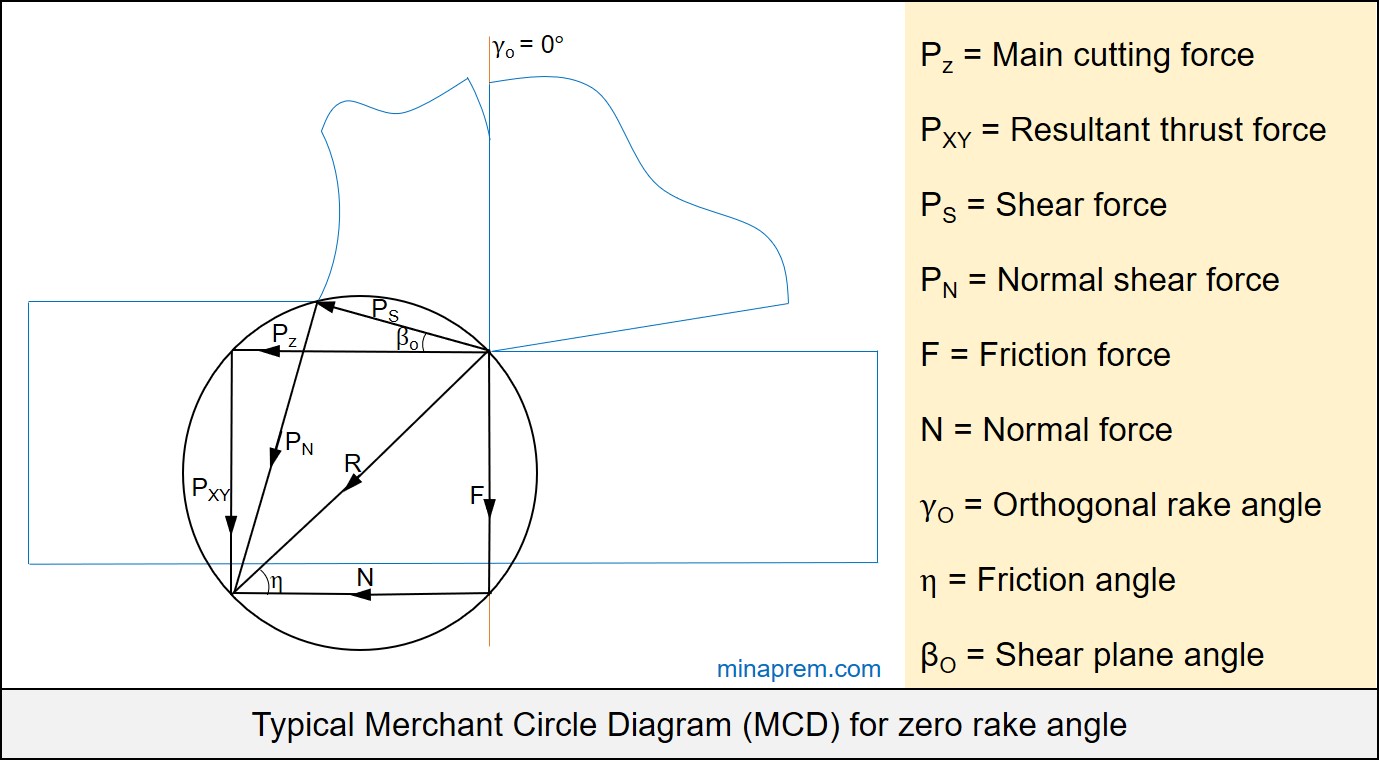
In the question, it is given that the tool has a zero rake angle (γ_O = 0°). When rake angle becomes zero, the main cutting force (P_Z) becomes parallel to the normal force (N), and also the resultant thrust force (P_XY) becomes parallel to the friction force (F). Therefore, P_Z P_XY F and N altogether constitute a rectangle. In question, two forces are given: P_Z = 500N and P_XY = 250N. Using these two values, the angle between P_Z and R can be calculated. Now since P_Z is parallel to N, so friction angle will be same. Coefficient of friction can now be calculated from the tangent of friction angle. Step by step calculation is given below.

Step-1: Calculate angle between P_Z and R

Consider the triangle made by P_XY P_Z and R. It is one right angle triangle as R is the diameter of the Merchant’s circle. P_Z is given as 500N and P_XY is given as 250N. So using simple trigonometry relationship, the required angle can be calculated. If angle between P_Z and R is θ (say), then:

\[\tan \theta  = \frac{{{P_{XY}}}}{{{P_Z}}}\]

\[\tan \theta  = \frac{{250}}{{500}} = \frac{1}{2}\]

\[\theta  = {\tan ^{ – 1}}\left( {\frac{1}{2}} \right) = 26.56^\circ \]

Step-2: Calculate friction angle (η)

Friction angle (η) is the angle between R and N, as shown in above image for MCD. Also, P_Z is parallel to the N due to zero rake angle. Hence, friction angle will be equal to the angle between P_Z and R. Therefore,

∴ Friction angle (η) = Angle between P_Z and R = 26.56°

Step-3: Calculate coefficient of friction (μ)

Tangent of friction angle gives the coefficient of friction. The friction angle (η) is calculated in previous step. So coefficient of friction can be calculated easily as shown below.

\[\mu  = \tan \eta \]

\[\mu  = \tan 26.56 = 0.5\]

Therefore, the coefficient of friction between tool and chip for this case is 0.5.