Calculate chip velocity from rake angle, shear angle and cutting velocity

Machining, Numerical

Question: The rake angle of a cutting tool is 15°, shear angle 45° and cutting velocity 35m/min. What is the velocity of chip along the tool face? [ISRO 2009]

Answer: Three velocity terms namely cutting velocity (VC), chip flow velocity (Vf) and shear velocity (VS) are associated with orthogonal machining of ductile material using a sharp cutting tool. These three velocity terms together constitute a vector triangle, which is also known as velocity triangle in machining. A typical velocity triangle is shown below.

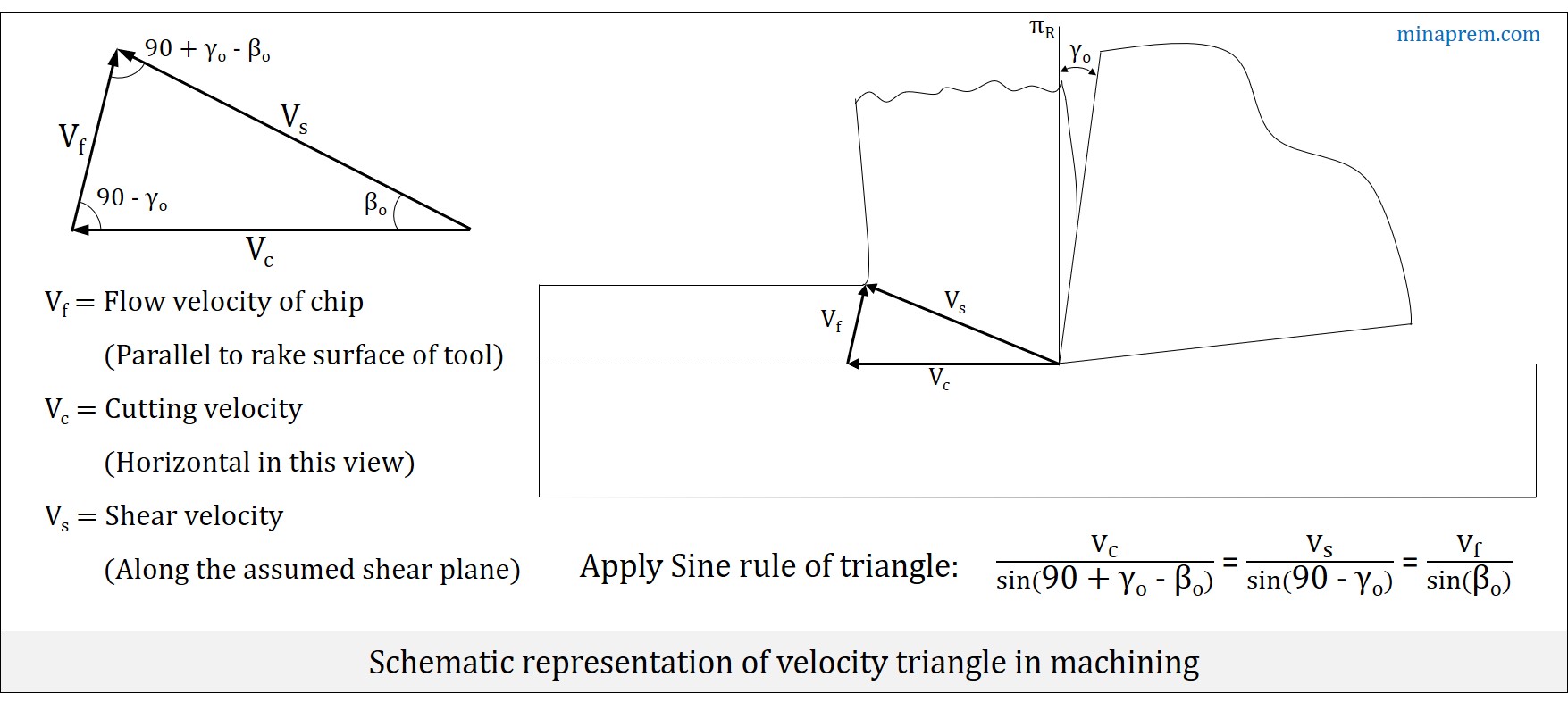
Schematic representation of velocity triangle in machining

The shear velocity (VS) is directed along the shear plane and thus makes an angle equal to shear angle (βO). The chip flow velocity (Vf) is directed along the rake surface of the cutting tool, and thus makes an angle equal to orthogonal rake angle (γO) with the reference plane (πR). Therefore, the angle between cutting velocity (VC) and chip flow velocity (Vf) is (90 – γO). Once two angles are known, the third angle can be calculated easily as sum of all three angles of any triangle is 180°. Application of Sine Rule on this velocity triangle leads to the following expression.

\[\frac{{{V_c}}}{{\sin \left( {90 + {\gamma _o} – {\beta _o}} \right)}} = \frac{{{V_s}}}{{\sin \left( {90 – {\gamma _o}} \right)}} = \frac{{{V_f}}}{{\sin {\beta _o}}}\]

Calculate velocity of chip along the tool face

As per the question, chip flow velocity (Vf) is required from the known values of orthogonal rake angle of a cutting tool, shear angle and cutting velocity. Here, γO = +15°, βO = 45°, and VC = 35m/min. Since shear velocity (VS) has no role in this case, so that part can be eliminated. Considering only chip flow velocity (Vf) and cutting velocity (VC), the general equation of velocity triangle for machining can be reduced to the following expression. Thereafter substitution of given values of corresponding parameters, the unknown parameter can be obtained easily. Detailed calculation is given below.

\[\frac{{{V_c}}}{{\sin \left( {90 + {\gamma _o} – {\beta _o}} \right)}} = \frac{{{V_f}}}{{\sin {\beta _o}}}\]

\[\frac{{35}}{{\sin \left( {90 + 15 – 45} \right)}} = \frac{{{V_f}}}{{\sin 45}}\]

\[{V_f} = \frac{{35\sin 45}}{{\sin 60}}\]

\[{V_f} = 28.58\]

Therefore, the intended velocity of chip along the tool face is 28.58 m/min.

Related posts:

  1. Determine shear angle from orthogonal rake angle and chip thickness ratio
  2. Calculate shear velocity in terms of rake angle, shear angle, cutting velocity
  3. Calculate shear angle using orthogonal rake angle, uncut and cut chip thickness
  4. Calculate shear strain from chip thickness ratio and rake angle
  5. Calculate shear strain from feed, chip thickness and rake angle
  6. Velocity triangle in machining – cutting velocity, chip velocity, shear velocity
  7. Calculate chip velocity from cutting speed, depth of cut and chip thickness
  8. Calculate shear angle for minimum shear strain with positive rake angle
  9. Determine shear plane angle and chip velocity in orthogonal turning
  10. Shear angle using rake angle, uncut chip thickness and nominal chip thickness