Calculate chip shear force from cutting and thrust forces and shear angle

Machining, Numerical

Question: In orthogonal cutting test, the main cutting force = 900 N, the thrust force = 600 N and chip shear angle is 30°. Calculate the chip shear force. [ESE 2003]

Solution: This problem on cutting force can be solved with the help of Merchant Circle Diagram (MCD). MCD is one vector representation of several cutting forces associated with orthogonal machining with a sharp tool. A typical MCD for positive orthogonal rake angle is sown below. Here the resultant force (R) is also the diameter of the circle.

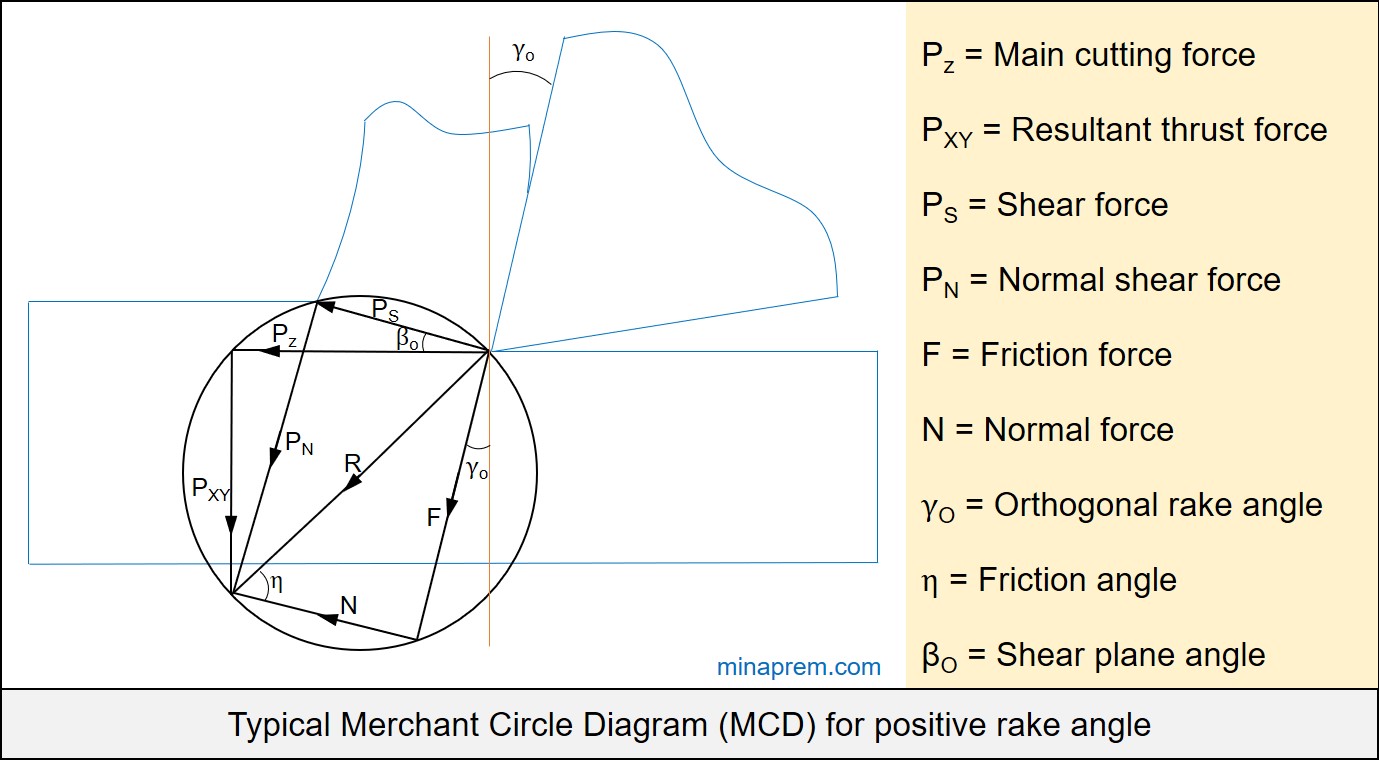
Typical Merchant Circle Diagram (MCD) for positive rake angle

In the given problem, main cutting force (PZ) and resultant thrust force (PXY) are given. Using these two values, the angle between PZ and R can be calculated. Also the value of resultant force (R) can be calculated. Now using the known value of R and corresponding angles, the value of chip shear force (PS) can be calculated easily. The steps followed here does not require any MCD formula to be remembered. It is based on simple geometry. Step by step calculation is discussed below.

Step-1: Calculate resultant force (R)

The triangle formed by R, PZ and PXY is one right angle triangle as R indicates the diameter of the Merchant’s Circle. Given, PZ = 900N and PXY = 600N. So consider the right angle triangle constituted by R, PZ and PXY. R can be calculated as follows.

\[R = \sqrt {{{\left( {{P_Z}} \right)}^2} + {{\left( {{P_{XY}}} \right)}^2}} \]

\[R = \sqrt {{{900}^2} + {{600}^2}}  = 1081.66N\]

Step-2: Find out angle between PZ and R

Once again consider the right angle triangle constituted by R, PZ and PXY. With the help of trigonometry, the angle between PZ and R can be calculated as follows. If this angle be θ, then

\[\tan \theta  = \frac{{{P_{XY}}}}{{{P_Z}}}\]

\[\tan \theta  = \frac{{600}}{{900}} = \frac{2}{3}\]

\[\theta  = {\tan ^{ – 1}}\left( {\frac{2}{3}} \right) = 33.69^\circ \]

Step-3: Calculate chip shear force (PS)

In question, the chip shear angle (βO) is given as 30°. Now consider the right angle triangle constituted by R, PS and PN. Here the value of R is already calculated. The angle between R and PS is (θ + βO) = (33.69° +30° ) = 63.69°. Therefore, the value of PS can be calculated easily as shown below.

\[\cos 63.69 = \frac{{{P_S}}}{R}\]

\[{P_S} = 1081.66 \times \cos 63.69 = 479.42N\]

Therefore, the chip shear force (PS) = 479.42 N

Related posts:

  1. Determine shear plane angle and chip velocity in orthogonal turning
  2. Calculate power consumption from coefficient of friction and thrust force
  3. Determine main cutting force, radial force, normal force and shear force
  4. Calculate chip velocity from rake angle, shear angle and cutting velocity
  5. Calculate shear angle using orthogonal rake angle, uncut and cut chip thickness
  6. Determine rake angle and normal force if main cutting force is perpendicular to friction force
  7. Calculate shear strain from chip thickness ratio and rake angle
  8. Calculate shear strain from feed, chip thickness and rake angle
  9. Calculate shear force and rate of heat generation at primary shear plane
  10. Calculate shear plane angle and shear strain in orthogonal cutting