In abrasive jet machining (AJM), high velocity abrasive jet is allowed to strike the work surface to remove material by impact erosion. For the sake of modeling it is assumed that only rigid abrasive particles partake in erosion action (carrier gas has no role in material erosion). Each particle creates an indentation of certain diameter and every particle equally participates in material removal action. In estimation of material removal rate (MRR) in AJM, it is assumed that for ductile materials, volume of material removed by single impact is equal to volume of the single indentation; whereas, for brittle materials, volume of material removed by single impact is equal to volume of hemispherical crater having diameter equals to chord length of the indentation. Mathematically, expression of MRR for ductile materials and brittle materials can be expressed as shown below.

• Read more: Estimation of MRR for ductile and brittle materials in AJM (Modeling).

Notation used

• U = Velocity of abrasive jet at the point of impact.
• H = Flow strength or hardness of work material.
• M_g = Mass flow rate of abrasive particles.
• ρ_g = Density of each abrasive particle.

Condition for equal MRR for ductile and brittle materials

Although abrasive jet machining is not suitable for soft materials (read why), it can be applied for ductile materials too utilizing optimum process parameters and suitable abrasives. There exists a specific jet velocity where MRR for ductile materials will be equal to that for brittle materials. From the above expressions it is axiomatic that MRR for ductile materials is proportional to square of jet velocity (V²); whereas for brittle materials it is proportional to V^1.5. The plot of variation of MRR with jet velocity for two types of materials is depicted below.

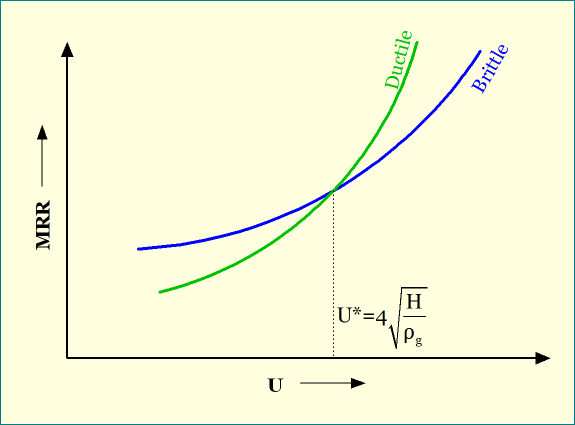
Therefore, if abrasive jet velocity is below this optimum level then MRR for brittle materials will be larger than that for ductile materials. The expression for this optimum velocity (U^*) can be mathematically derived by equating corresponding MRR formulas, as described below. For same MRR, we may write:

\({MRR_{ductile}} = {MRR_{brittle}}\)

or, \({1 \over 2}{{{M_g}{U^2}} \over H} = {{{M_g}{U^{3/2}}} \over {{\rho _g}^{1/4}{H^{3/4}}}}\) [Neglecting 1.04 term]

or, \({{{U^2}} \over {{U^{3/2}}}} = {{2H} \over {{\rho _g}^{1/4}{H^{3/4}}}}\)

or, \({U^{1/2}} = {{2{H^{1/4}}} \over {{\rho _g}^{1/4}}}\)

or, \(U = 4\sqrt {{H \over {{\rho _g}}}}  = {U^ * }\)

$$∴{U^ * } = 4\sqrt {{H \over {{\rho _g}}}} $$

Reference

• Book: Nonconventional Machining by P. K. Mishra (Narosa Publishing House).