Question: Mild steel is being machined at a cutting speed of 200 m/min with a tool rake angle of 10°. The width of cut and uncut thickness are 2 mm and 0.2 mm, respectively. If the average value of co‐efficient of friction between the tool and the chip is 0.5 and the shear stress of the work material is 400 N/mm², then determine: [ESE 2005]

(i) The shear angle

(ii) Cutting and thrust components of the force.

---

Solution: This problem can be solved with the help of Merchant Circle Diagram (MCD). The work material is given as mild steel, which is a ductile material (as mild steel is the alloy of just about 0.2wt% carbon in iron). So the Lee Shafer’s formula of ductile material can be employed. Here the rake angle of the cutting tool is also given as positive. A typical MCD for positive rake is shown below. Step by step solution of this problem is described thereafter.

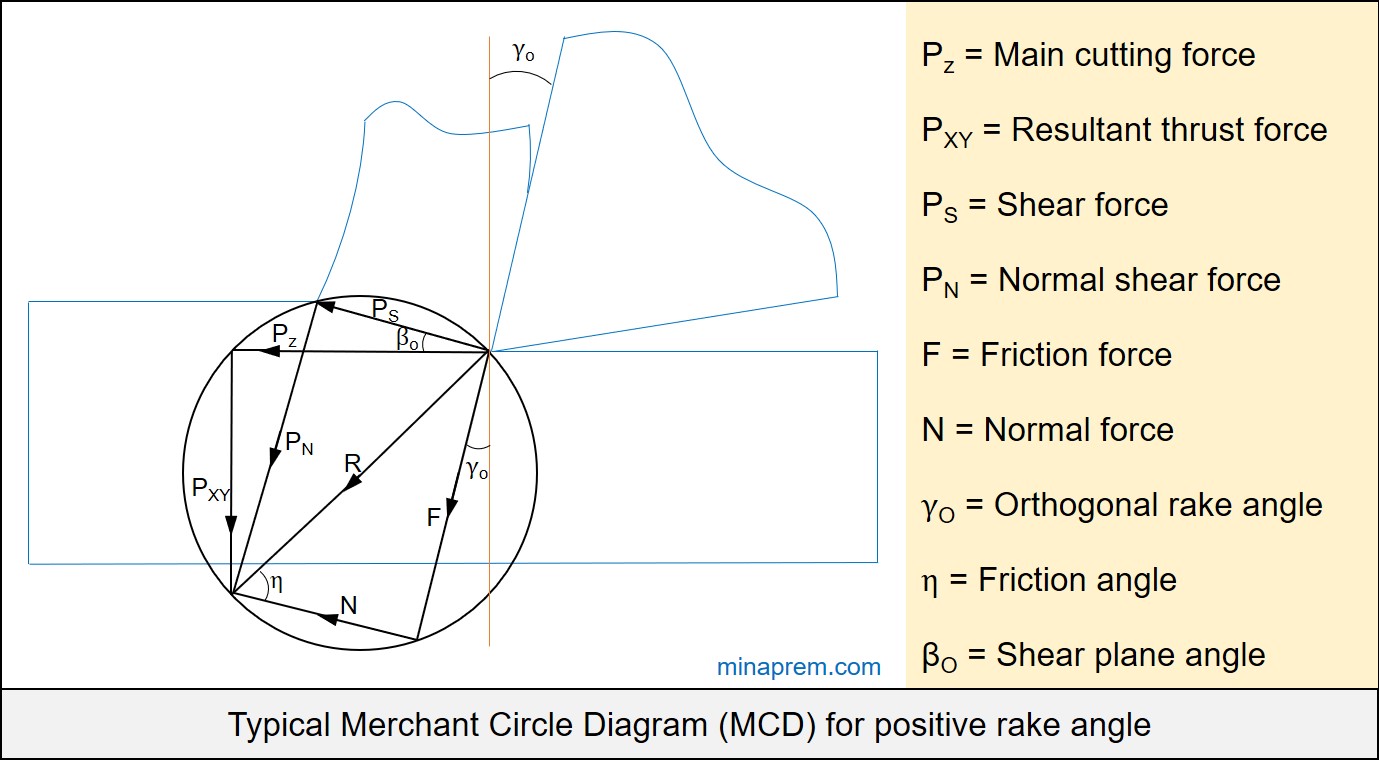
Given values in question

Cutting velocity (V_C) = 200 m/min

Orthogonal rake angle (γ_O) = +10°

Width of cut (b) = 2 mm

Uncut chip thickness (a₁) = 0.2 mm

Average co‐efficient of friction (μ) = 0.5

Shear strength of work material (τ_S) = 400 N/mm²

Step-1: Calculate friction angle (η)

From the basic physics it is well-known that tangent of the friction angle (η) gives the co‐efficient of friction (μ). Here, co‐efficient of friction is given in question, so friction angle can be calculated as shown below.

\[\mu  = \tan \eta \]

\[\eta  = {\tan ^{ – 1}}\mu \]

\[\eta  = {\tan ^{ – 1}}0.5 = 26.56^\circ \]

Step-2: Find out shear angle (β_O)

Lee Shafer’s formula gives a relationship among orthogonal rake angle of the cutting tool (γ_O), friction angle (η) and shear angle (β_O). However, it is applicable only if the work material is ductile. Here rake angle and friction angle are known and also the work material is mild steel (ductile). So let us apply Lee Shafer’s formula to get the unknown shear angle.

Lee Shafer’s formula: β_O + η – γ_O = 45°

or, β_O + 26.56° – 10° = 45°

or, β_O = 28.44°

Therefore, the shear angle for the given case is 28.44° (Answer).

Step-3: Determine shear force (P_S)

To apply MCD for calculating any force, we need at least one force component to be known along with three relevant angles. Here no force value is directly given in question. However, from other given data, the shear force can be calculated. Shear force indicates the force required for shearing of the workpiece material along the shear plane under orthogonal machining. This force can be expressed by multiplying shear area (A_S) with shear strength of the workpiece material (τ_S). This shear area (A_S) is once again a function of uncut chip thickness (a₁), shear angle (β_O) and width of cut (b). Since all these are known, so shear force can be calculated easily, as described below.

\[{P_S} = {\tau _S}{A_S}\]

\[{P_S} = {\tau _S}\left( {\frac{{{a_1}}}{{\sin {\beta _O}}} \times b} \right)\]

\[{P_S} = 400 \times \frac{{0.2}}{{\sin 28.44}} \times 2\]

\[{P_S} = 336N\]

Step-4: Determine resultant force (R)

Here, the cutting and thrust components of the force are required to calculate. These can be calculated simply by using relevant formula in terms of shear force. However, you need to memorize complicated formula. The steps discussed below does not required any formula to be memorized, although it is little bit lengthy. It is based on simple trigonometric relationships.

So let us consider the triangle constituted by P_S, P_N and R. It is one right angle triangle as R is the diameter of the Merchant’s Circle (basic property of MCD). Now, the value of P_S is known. A close look to the MCD also reveals that the angle between P_S and R is equal to (β_O + η – γ_O). Therefore, R can be calculated as follows.

\[\cos \left( {{\beta _O} + \eta  – {\gamma _O}} \right) = \frac{{{P_S}}}{R}\]

\[R = \frac{{336}}{{\cos \left( {45} \right)}} = 475.2\]

Step-5: Determine main cutting force (P_Z)

Now consider the triangle made by P_Z P_XY and R. It is also one right angle triangle. The angle between P_Z and R is (η – γ_O). The value of R is also calculated earlier. So from the basic trigonometric relation, the vale of P_Z can be calculated easily, as shown below.

\[\cos \left( {\eta  – {\gamma _O}} \right) = \frac{{{P_Z}}}{R}\]

\[{P_Z} = R\cos \left( {\eta  – {\gamma _O}} \right)\]

\[{P_Z} = 475.2 \times \cos \left( {26.56 – 10} \right)\]

\[{P_Z} = 455.49N\]

Therefore, the main cutting force is 455.49 N (Answer)

Step-6: Determine thrust cutting force (P_XY)

Once again consider the right angle triangle made by P_Z P_XY and R. Using the R value and angular relationship, the value of P_XY can be calculated easily, as described below.

\[\sin \left( {\eta  – {\gamma _O}} \right) = \frac{{{P_{XY}}}}{R}\]

\[{P_{XY}} = R\sin \left( {\eta  – {\gamma _O}} \right)\]

\[{P_{XY}} = 475.2 \times \sin \left( {26.56 – 10} \right)\]

\[{P_{XY}} = 135.44N\]

Therefore, thrust force is 135.44 N (Answer).