Question: In an orthogonal cutting test, the cutting force and thrust force were observed to be 1000 N and 500 N, respectively. If the rake angle of tool is zero, what will be the coefficient of friction in chip‐tool interface? [ESE 2000]

Solution: For an orthogonal machining, the rake angle of the cutting tool is given as zero. The cutting force and thrust force values are also given. Using these values, we need to calculate coefficient of friction at chip‐tool interface. Since coefficient of friction can be expressed as the tangent of friction angle, so our objective is to find out friction angle using Merchant Circle Diagram (MCD). A typical MCD for zero rake tool is shown below.

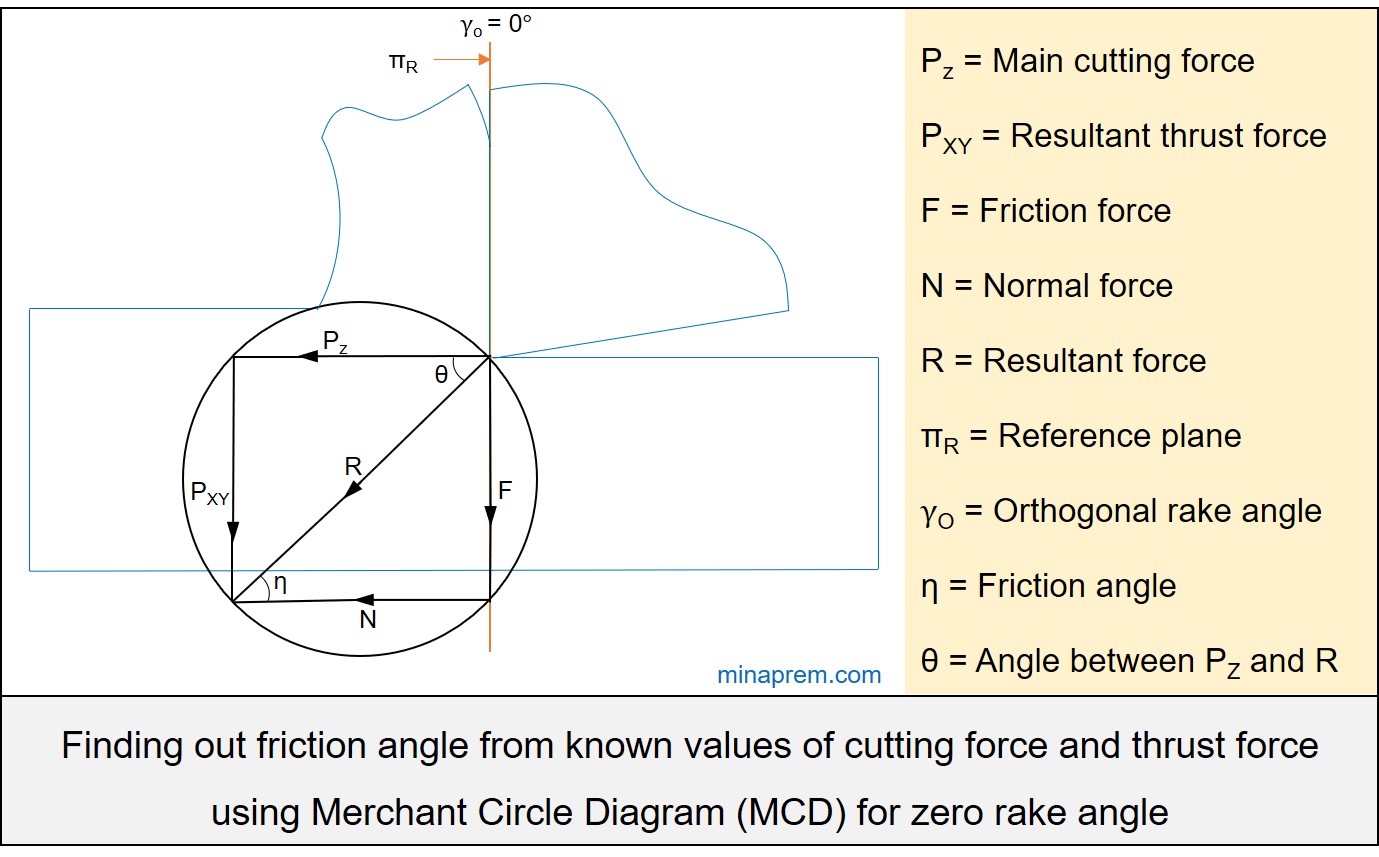
When rake angle becomes zero, four forces—main cutting force (P_Z), thrust force (P_XY), normal force (N) and friction force (F)—together constitute a rectangle. Thus, P_Z and N become parallel to each other, and also P_XY and F become parallel to each other. On the other hand, the angle between R and N is called the friction angle, which we need to find out. Since P_Z and N are parallel, so the angle between P_Z and R is also same with the friction angle. Now let us calculate this angle from the given values.

Step-1: Find out angle between P_Z and R (i.e. θ)

Consider the triangle made by P_Z P_XY and R. It is one right angle triangle as R is the diameter of the Merchant’s circle. Here, cutting force and thrust force values are given: P_Z = 1000 N and P_XY = 500 N. So the required angle θ can be calculated easily using basic trigonometric relationship for that right angle triangle, as described below.

\[\tan \theta  = \frac{{{P_{XY}}}}{{{P_Z}}}\]

\[\tan \theta  = \frac{{500}}{{1000}} = \frac{1}{2}\]

\[\theta  = {\tan ^{ – 1}}\left( {\frac{1}{2}} \right) = 26.56^\circ \]

Step-2: Determine the angle of friction (η)

As mentioned earlier, P_Z and N are parallel for zero rake angle. Therefore, friction angle (η) must be same with the angle θ as calculated in previous step.

∴ Friction angle (η) = θ = 26.56°

Step-3: Calculate coefficient of friction (μ)

Tangent of the angle of friction is known as co-efficient of friction. Since angle of friction is already calculated, so co-efficient of friction can also be find out easily, as described below.

\[\mu  = \tan \eta \]

\[\mu  = \tan 26.56 = 0.5\]

Therefore, the co-efficient of friction between tool and chip for this case is 0.5.