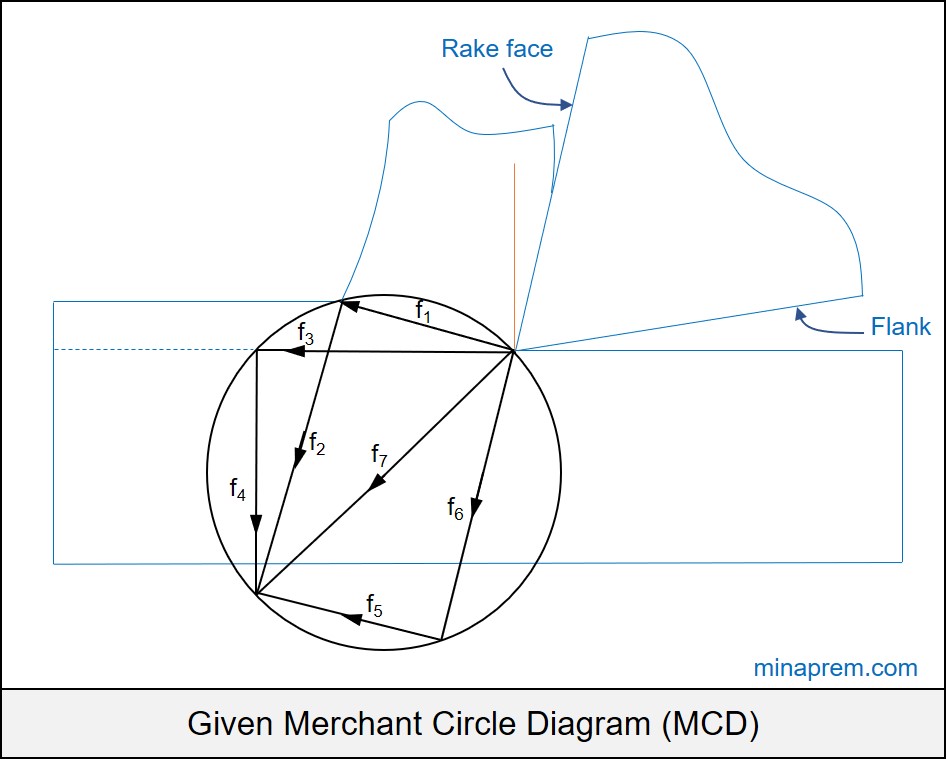
Question: The Merchant circle diagram showing various forces associated with a cutting process using a wedge-shaped tool is given in the adjacent Figure. The coefficient of friction can be estimated from the ratio: [GATE 2017]

(i) f₁ / f₂

(ii) f₃ / f₄

(iii) f₅ / f₆

(iv) f₆ / f₅

Solution: Merchant Circle Diagram (MCD) is the graphical representation of various forces associated with an orthogonal machining operation. It displays shear force (P_S), normal shear force (P_N), main cutting force (P_Z), resultant thrust force (P_XY), friction force (F), normal force (N) and a resultant force (R). One characteristics of MCD is that the resultant (R) is the diameter of the circle.  A typical Merchant Circle Diagram (MCD) for a tool having positive orthogonal rake angle is shown below.

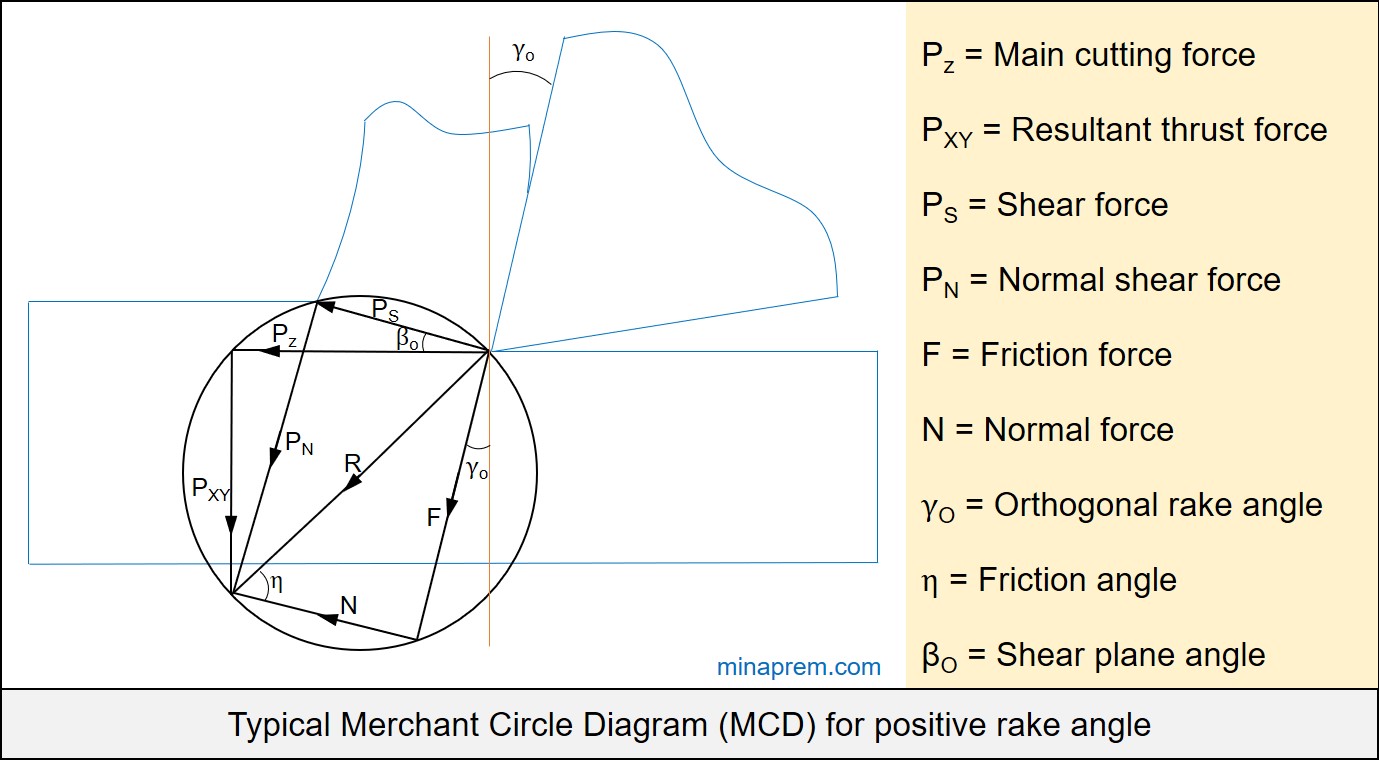
In MCD there exist three right angle triangles all having one common arm:

1. Triangle formed by P_S, P_N and R
2. Triangle formed by P_Z, P_XY and R
3. Triangle formed by F, N and R

Now the angle between N and R provides the friction angle (η). Tangent of the friction angle gives the co-efficient of friction (i.e. μ = tanη). So if we consider the right angle triangle formed by F, N and R, then the following can be written:

\[\mu  = \tan \eta  = \frac{F}{N}\]

Now let us compare with the given Merchant Circle Diagram (MCD) where the forces are denoted by different symbols. So the coefficient of friction for the given case can be expressed as follows.

\[\mu  = \tan \eta  = \frac{{{f_6}}}{{{f_5}}}\]

Hence, option (iv) is the correct answer.