Machining or metal cutting is one important aspect of the production system. Ultimate objecting of machining is to give intended shape, size and finish by gradually removing material from workpiece. Relevant steps such as removal of material, setting the job and cutting tool, and dispatching the machined job consume substantial amount of time, which are at least not negligible. For effective planning of the entire production, overall machining or cutting time must be incorporated.

Now-a-days the primary goal of industries is to manufacture the product at a faster rate but at minimal cost and that too without sacrificing product quality. As long as conventional machining is utilized, in order to fulfill first requirement (faster production rate), the cutting speed and feed rate should have to be increased. However, this may lead to reduced cutting tool life due to faster wear rate and higher heat generation. Hence, cutting tool is required to change frequently, which will ultimately impose a loss for the industry as a result of idle time for changing tools. Cost of tool is also not negligible. Therefore abrupt increase of cutting speed and feed rate is not a feasible solution; rather, an optimization is necessary.

Overall machining time and cost

In today’s competitive market, time is equivalent to cost. Basically overall or total machining time (T_m) is the summation of three different time elements closely associated with the machining or metal cutting process. These three elements include—actual cutting time (T_c), total tool changing time (T_ct) and other handling or idle time (T_i). Beside these three time elements, cost of cutting tool is also required to incorporate for any optimization. All these time or cost elements, except handling time, are affected by the variation of cutting speed and feed rate as explained below. Mathematically, total time for machining (T_m) can be expressed as:

T_m = T_c + T_ct + T_i

What is actual cutting time (T_c)?

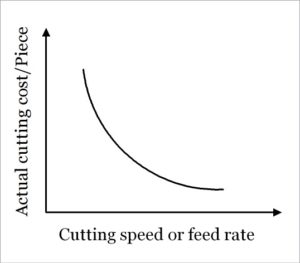As the name suggests, cutting time is the time taken during actual material removal action, i.e., from the beginning of chip production to the end for uninterrupted machining. In case of any planned or unplanned stoppage in cutting, the pause duration will not come under this time element. Therefore, increase in cutting speed and feed rate will result in reduction of actual cutting time as material removal rate (MRR) will increase. Hence, cost associated with cutting time will decrease if speed or feed is increased. The adjacent diagram depicts how cost associated with the actual cutting time varies with speed or feed employed during machining.

Mathematical expression of actual cutting time

If, L_c is the total length of cut (mm), N is the spindle speed (rpm) and s is the feed rate (mm/rev), then estimated uninterrupted cutting or machining time can be expressed as:

Actual Cutting Time (T_c) = \({{{L_c}} \over {N.s}}\)

In most of the cases, where either workpiece or cutting tool is rotating, the spindle speed (N) and cutting velocity (V_c) are interchangeable. However, cutting velocity also depends on the diameter of the job/cutter (D). Cutting velocity can be expressed, in terms of speed and diameter of job or cutter (whichever is rotating), as follows. For better understanding of this conversion, you may read: Cutting speed and cutting velocity in machining.

Cutting velocity (V_c) = \({{\pi DN} \over {1000}}\)

In case of turning or milling, actual cutting time can be expressed as:

\({T_c} = {L \over {N.s}}\)

\({T_c} = {L \over {\left( {{{1000{V_C}} \over {\pi D}}} \right)S}}\)

\({T_c} = {{\pi DL} \over {1000{V_C}}}\)

What is tool changing time (T_ct)?

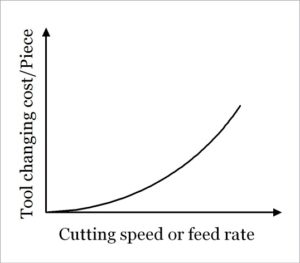Every time a tool has certain life within which it can perform satisfactorily; and thus replacement or re-sharpening is required to perform once tool life exceeds. Cutting or machining action is also required to pause for certain time. Increase in cutting speed or feed rate will reduce tool life (evident from Taylor’s Modified Tool Life Equation) and thus frequent tool changing will be desired. This unplanned and frequent interruption in machining will impose loss to the industry. The adjacent diagram depicts how cost associated with the tool changing time varies with the speed or feed employed during machining.

Mathematical expression of tool changing time

Since every cutting tool has certain finite life (called Tool Life – TL), so it may require changing the cutting tool before the specific operation is completely done. Sometime tool is needed to change multiple times. Therefore, the number of times tool changing is required depends on the actual machining time.

If TCT is the average time required by the operator or automation system (such as automatic tool changer – ATC) to change the tool, then, mathematically, tool changing time (T_ct) can be expressed as follows. Basically it is the multiplication of tool changing time for one tool change (TCT) and the number of times such tool changing is desired within the specified cutting time (T_c).

$${T_{ct}} = \left( {{{{T_c}} \over {TL}}} \right) \times TCT$$

What is part handling time or idle time (T_i)?

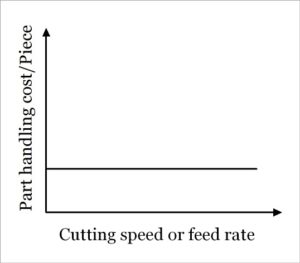This time element depends on the workpiece and its configuration as well as material handling system employed. It takes care of loading and unloading of job and is independent of the cutting velocity or feed rate employed during machining. It is frequently termed as idle time as machine remains idle during loading and unloading. The adjacent diagram depicts how cost associated with the idle time varies with the speed or feed employed during machining. As it is independent of cutting parameters, its value is required to obtain directly from database, direct measurement or experience.

Tooling cost – cost of the cutting tool

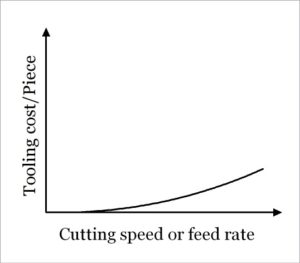Although it is not directly associated with cutting velocity, tooling cost also contributes in overall machining economy. If higher speed or feed is employed, the result will be faster tool wear and reduced tool life, which will ultimately multiply expenditure as more tools are required for cutting same length.  The adjacent diagram depicts how tool cost varies with the speed or feed employed during machining.

Tooling cost can be calculated by multiplying the price of individual cutting tool (K₂) with the quantity of tool required. Quantity of tool required can again be determined by dividing actual machining time by tool life. Mathematically, tooling cost can be determined by the formula:

Tooling cost = \(\left( {{{{T_c}} \over {TL}}} \right) \times {K_2}\)

Overall machining time and cost

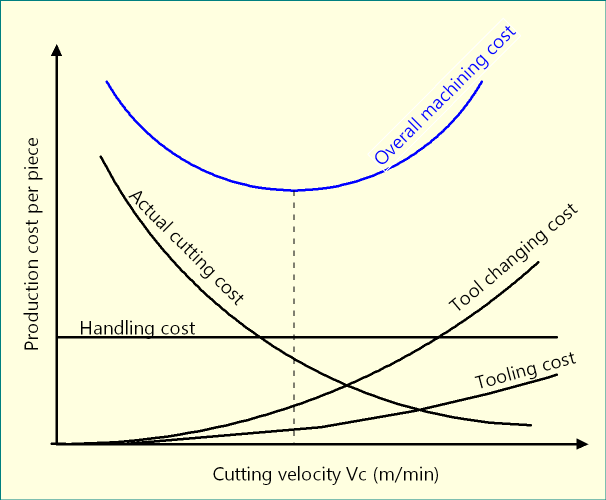
Since every time elements pertinent to machining contributes towards machining cost, so some factors are required to convert time to cost. On the basis of these factors, time elements can be converted to cost elements and estimation of machining economy becomes easier. Such factors include:

• K₁ = Cost-time conversion factor for machining
• K₂ = Cost-time conversion factor for tool sharpening or price of new tool.

Therefore, overall machining cost per piece (C_p)

= (Actual cutting cost/piece) + (Tool changing cost/piece) + (Handling cost/piece) + (Tooling cost/piece)

= K₁ {(Actual cutting time/piece) + (Tool changing time/piece) + (Handling time/piece)} + K₂ {(Tooling cost/piece)}

= K₁ {T_c + T_ct + T_i} + \(\left( {{{{T_c}} \over {TL}}} \right) \times {K_2}\)

Finding out economic condition and Gilbert’s Model

Undoubtedly the final thing is to find out the optimum condition for either maximizing profit or minimizing time requirement. For paper based optimization, only cutting velocity or speed is considered in order to keep the analytical process less complicated. Moreover, cutting velocity is the main parameter that affects machining performance. A number of constraints can be handled effectively using computer programming based optimization techniques.

Now there exist a number of objectives for optimization, among which Gilbert’s Model (1952) for Maximum Production Rate and Minimum Production Time are more prominent. These models are based on the Taylor’s Tool Life equation, which consider only cutting velocity to determine tool life. Various economic models for optimizing machining process parameters for different objectives are provided below. You may follow the links for detailed analysis of such optimization.

• Optimum velocity & tool life for maximum production rate
• Optimum velocity and tool life for minimum production cost

Reference

• Book: Metal Cutting: Theory And Practice by A. Bhattacharya (New Central Book Agency).
• Book: Machining and Machine Tools by A. B. Chattopadhyay (Wiley).